| Возьмем за основу распределительный закон. Попробуйте формулировать гипотезы, как связана операция извлечения корня с арифметическими операциями. |
  |
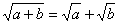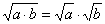a (b + c) = a b + a c |
| Давайте проверим вторую гипотезу. |
|
|
| Вспомним определение квадратного корня. |
Квадратным корнем из неотрицательного числа а называется такое неотрицательное число, квадрат которого равен a . |
|
| Какие числа по знаку стоят в левой и правой части гипотезы 2? |
Оба числа неотрицательны, число стоящее в левой части неотрицательное по определению квадратного корня. В правой части как произведение квадратных корней. |
|
| Возведите правую и левую часть гипотезы в квадрат. |
Левая и правая часть равны а• b |
|
| Какое теоретическое положение позволило нам это утверждать? |
Одно из свойств степени с натуральным показателем. |
|
| Теперь давайте проанализируем полученные результаты. Рассмотрим правую часть гипотезы. Как мы выяснили она неотрицательна, кроме этого будучи возведенной в квадрат дает .выражение стоящее под знаком корня в левой части. Сделайте выводы из всего вышесказанного. |
Число  удовлетворяет всем условиям определения арифметического квадратного корня из неотрицательного числа. |
|
| Как связаны выражения стоящие в левой и правой части гипотезы? |
Они равны. |
|
| Доказали ли мы эту гипотезу? |
Да |
|
| В математике принято каждое утверждение формулировать в виде теоремы. Фактически мы доказали теорему о связи операции извлечения квадратного корня и операции умножения. Попробуйте сформулировать эту теорему. |
Ученики пытаются сформулировать теорему. |
|
| Откройте учебники и сравним нашу формулировку с формулировкой в учебнике. |
|
|
| Такая формулировка, которая приведена в учебнике в математике носит название формулировки в категоричной форме. Кроме этого теоремы принято формулировать используя конструкцию «если… то», такая форма называется условной. |
|
|
| Попробуйте переформулировать теорему, используя слова «если… то». |
Ученики пытаются переформулировать теорему в условной форме. |
|
Формулировка теоремы в условной форме будет выглядеть так: «если a и b неотрицательные числа, то справедливо равенство  ». |
|
|
| Выделите в формулировке теоремы условие и заключение |
Ученики выделяют условие теоремы и заключение теоремы. |
|
| Сформулируйте обратное утверждение. |
Ученики формулируют теорему обратную данной: «если верно равенство  , то a и b неотрицательные числа». |
|
| Верна ли эта теорема. |
Да, верна. |
|
| Объясните почему. |
Ученики дают свои объяснения этому факту. |
|
| Действительно если равенство верно, то a , b числа неотрицательные числа и это следует из определения квадратного корня. |
|
|
| Эта теорема носит название свойства квадратных корней. |
|
|
| Равенство останется верным если подкоренное выражение будет представлять собой арифметическое выражение. |
|
|
Решите пример.
|
|
|
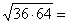
| Какой теоретический факт позволит нам решить этот пример? |
Только что изученная теорема.
(ученики решают этот пример) |
|
Решите пример  |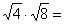
|
|
| Какой теоретический факт позволит нам решить этот пример? |
Та же теорема. |
|
| Почему для решения этой задачи мы можем использовать свойство квадратных корней? |
Потому что мы доказали равенство, а его можно использовать в обе стороны. |
|
Решите пример  |
(если вызовет затруднения, то можно представить дробь в виде произведения) |
|
| Как вы думаете существует ли связь между операцией извлечения квадратного корня и операцией деления. |
да |
|
| Давайте сформулируем гипотезу. |
Ученики пытаются сформулировать гипотезу о связи деления и извлечения корня. |
|
Формулировка теоремы: «если  и  , то справедливо равенство  .» |
|
|
| В начале урока мы выдвинули еще одну гипотезу, вспомните какую? |
 . |
|
| Как вы математике устанавливается справедливость какого, то утверждения? |
Путем доказательства |
|
| А как устанавливается, что данное утверждение не верно? |
Для этого надо привести контрпример. |
|
| Вспомним пример 1 в начале урока, попытайтесь его решить используя нашу гипотезу. |
Ученики пытаются решить данное задание используя сформулированную в начале урока гипотезу. |
Ученики в тетрадях пытаются решить этот пример. |
| Как видите это не верно. Поэтому свойства аналогичному свойству относящемуся к умножению нет. |
|
|
