Урок по теме "Применение четности и нечетности функции к построению графиков функций". 9 кл. Алимов и др.

Тема: Применение четности и нечетности функции к построению графиков функций.

Учебная задача: Рассмотреть возможность использования свойства четности/нечетности функции, при построении ее графика.

В результате ученик:

1. Знает определение четной и нечетной функции.
2. Знает, что график четной функции симметричен относительно оси Оу.
3. Знает, что график нечетной функции симметричен относительно начала координат.
4. Знает, что график функции общего вида не симметричен относительно оси Оу и начала координат.
5. Знает, что использование четности/нечетности функции позволяет сократить количество вычислений при построении графика функции.
6. Умеет применять свойство четности/нечетности функции при построении графиков функций.

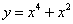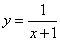
Слова учителя Слова учеников Записи на доске и в тетрадях Мотивационно-ориентировочный этап Какая функция называется четной? Функция называется четной, если для любого x из области определения функции выполняется Из предложенных функций выбрать четную функцию. Ученики дают ответ №1   Чем вы пользовались при решении данной задачи. Мы воспользовались определением четной функции.   Объясните, как вы решали данное задание? Мы проверили справедливость равенства . Оно выполняется только в первом случае.   Какая функция называется нечетной? Ученики дают определение. Функция называется нечетной если для любого х из области определения функция выполняется равенство   Из предложенных функций выбрать нечетную функцию. Ученики дают ответ №2.   Как вы установили, что функция №2 является нечетной. Мы воспользовались определением нечетной функции. Проверили выполнимость равенства . Оно верно только для функции №2.   Как вы считаете, свойство четности или нечетности присущи каждой функции? Нет, существуют функции как не являющиеся четными, так и нечетными.   Как мы называем такие функции? Такие функции в математике принято называть функциями общего вида.   Какие функции мы называем функциями общего вида? Функции которые и не четны и не нечетны.   Приведите пример такой функции. Это функция №3.   Как выглядит график четной функции? Он симметричен относительно оси Оу.   Как выглядит график нечетной функции? Он симметричен относительно начала координат.   Как выглядит график общего вида? ???? Но он не симметричен относительно оси Оу и начала координат.   Т.е. график четной/нечетной функции обладает свойством симметричности, а график функции общего вида таким свойством не обладает.     Давайте решим следующую задачу: Построить график функции 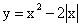.     Какие вам известны способы построения графика функции? По точкам.   Посмотрите на вид функции, где при вычислении функции могут быть допущены ошибки? При вычислении модуля!   Как мы можем уменьшить вероятность вычислительной ошибки? Научиться считать. Сократить количество вычислений.   Давайте попробуем найти такой способ.     Итак, как вы думаете, чем же мы будем заниматься на этом уроке? Найдем   А каким из недавно изученных нами свойств функций, обладает данная функция? Предполагаемые ответы Данная функция четная Данная функция нечетная.   Давайте проверим, является ли данная функция четной? Ученики проверяют и убеждаются, что функция обладает свойством четности.   Как ведет себя график четной функции? Он симметричен относительно оси Оу.   Подумайте, как можно воспользоваться этим свойством? Ученики предполагают, что можно построить график функции при , а затем отобразить симметрично оси Оу.   Итак, как вы думаете, чем же мы будем заниматься на этом уроке? Найдем способ применения свойств четности/нечетности при решении задач.   Запишите в тетради тему сегодняшнего урока: Применение четности и нечетности функции к решению задач. Ученики записывают в тетрадях тему урока.