- Да, а для этого нам с вами нужно решить 1-ну простую задачу. Но вначале, напомните мне формулу нахождения площади прямоугольника |
-  . . |
- Итак, приготовьтесь внимательно слушать, кому что не понятно – поднимаем руку, записывать весь ход решения задачи.
Открыли рабочие тетради, записали число, классная работа.
В своих тетрадях напишите «Задача» и зарисуйте, аналогичный изображённому на доске, прямоугольник, укажите на рисунке значение площади этого прямоугольника и одной известной его стороны – ширины прямоугольника. Посмотрите на рисунок – схему, сформулируйте вопрос задачи. |
- Найти длину прямоугольника. |
- Правильно. Запишем: «Найти: длина (сторона) прямоугольника. Решение».
Итак, какое равенство мы получим, подставив известные данные задачи в формулу нахождения площади прямоугольника? |
- 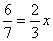 |
- Запишем полученное рав-во. Теперь выразим х , для чего необходимо так преобразовать рав-во, что бы справа остался один х , тогда слева будет его значение. Скажите, произведение какого числа на х даст нам в результате просто х ? |
- произведение 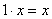 |
- На что же мы должны домножить правую половину равенства, чтоб вместо 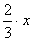 получить получить  ? ? |
- умножить на взаимно обратную для 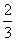 дробь: дробь:
 . .
|
- Так, справа мы получили х, при этом умножив правую часть равенства на  . На что же мы должны умножить и левую часть, что бы не нарушилось равенство? . На что же мы должны умножить и левую часть, что бы не нарушилось равенство? |
- Тоже на  . . |
- Что получим при этом? |
-  |
- Итак, какое равенство мы получили в результате? |
- 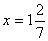 |
- Каков же ответ задачи? |
- Длина прямоугольника  . . |
- Вновь обратимся к исходному равенству. Какой компонент действия нам здесь был не известен? |
- Один из множителей произведения. |
- Вспомните правило нахождения неизвестного множителя, чему он равен в нашем случае? |
- Множитель равен частному от деления площади прямоугольника на известную сторону. |
- Запишем это. 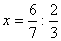 . Таким образом мы получили следующие два равенства, обратите внимание на доску, с одной стороны (показывает указкой) . Таким образом мы получили следующие два равенства, обратите внимание на доску, с одной стороны (показывает указкой)  , с другой , с другой  . Какой отсюда мы можем сделать вывод о том, как нужно делить одну дробь на другую? . Какой отсюда мы можем сделать вывод о том, как нужно делить одну дробь на другую? |
- Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю. |
- Правильно. В конце решённой задачи записываем полученный результат. С новой строки запишем правило: «Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю». Ещё раз повторим правило.
|
- Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю. |
- Познакомившись с новым правилом, что дальше мы с ним будем делать. |
- Рассмотрим его практическое применение. |
- Верно. Записываем в своих тетрадях №580 и решим примеры под буквами: а,б,в,г,ж,е,л,н. |
|
Учитель по очереди вызывает учеников к доске, те решают пример и вслух для всего класса говорят решение. Те в классе, кто идёт в таком же ритме, сверяются с доской, кто хорошо разобрался с новым правилом не дожидаясь весь класс, делает весь номер 580 (а,б,в,г,ж,е,л,н) и затем начинает выполнять дополнительное задание 583. |

